Can you solve this probability question?

A colleague asked me the following probability question:

Suppose I have N empty boxes and in each one I can place a 0 or a 1. I randomly choose n boxes in which to place a 1. If I start from the first box, what is the probability that the first 1 I find will be in the mth box?

This is depicted in the following graphic:

and we’re interested in the probability that the first 1 (reading from the left) is in, say, the third box.

I’m sure there must be a really nice form to the solution, but I can’t come up with one. The best I can do is the following slightly clunky one – any better ideas?

The probability of the first 1 being in the mth box is equal to the number of configurations where the first 1 is in the mth box, divided by the total number of configurations. The total number of configurations is given by:

and the number of configurations that have their first 1 in the mth box is equal to the subset of configurations that start 0,0,0,…,0,1. This is the same as the number of configurations of (n-1) 1s in (N-m) boxes, i.e. the different ways of building the sequence after the first 1:

So, the probability of the mth being the first 1 is:

Here’s what it looks like for a few different values of n, when N=100:

n=2:

n=5:

n=20:

which make sense – the more 1s you have, the more likely you’ll get one early. So, can anyone produce a neater solution? I’m sure it’ll just involve transforming the problem slightly.

Footnote: because the first one has to occur somewhere between the 1st and (N-n)th position,

and therefore:
,
which seems surprising to me. Although I don’t know why.

Footnote2: Here’s another way of computing it, still a bit clumsy. The problem is the same as if we had N balls in a bag, n of which are red and (N-n) of which are black. If we start pulling balls out of the bag (and not replacing them), the probability that the first red one appears on the mth draw is equal to the probability of drawing m-1 black ones and then drawing one red one. The first probability can be computed from the hyper-geometric distribution as:

and the second probability is just equal to the probability of picking one of the n reds from the remaining N-(m-1) balls:

So the full probability is:

which is arguably messier than the previous one.

Was Murray unlucky?

Andy Murray played Rafael Nadal today in the semi-final of the ATP tour finale at the O2 arena in London. Nadal won a great match, 7-6 (7-5), 3-6, 7-6.

Here are the match stats (couldn’t work out how to generate a permanent link to this):

Murray won the most points (5 more than Nadal), but still lost the match.

The other numbers near the bottom of the table tell us how many points each player won when serving and when receiving. Murray served 114 points of which he won 78; Nadal served 109 of which he won 73.

I’ve been considering building a statistical model for a tennis match for a while. A model is a mathematical representation of something in the world (e.g. a tennis match). With a good model, we can learn something about the match that perhaps isn’t immediately obvious and maybe predict what might happen in the future.

The number of points won when serving/receiving could form the basis of a simple model of a tennis match. Murray won 68.4% of the points when he served, and 33.0% of the points when Nadal was serving. Using this information, and a knowledge of the tennis scoring system, it is possible to generate potential matches: for each point, we flip one of two dodgy coins (depending on who is serving) and if it lands heads, we award the point to Murray. The first coin should be designed to land heads 68.4% of the time, the second 33.0% of the time. This would be time-consuming, but fortunately, it is the kind of thing that is very fast on a computer.

I’ve generated 10,000 matches in this way, of which Murray won 5753 (57.5%). In other words, if this model is reasonably realistic (more on this later), then we would expect Murray to win more often than lose if they played at the same level (served and received as well as they did today) in the future.

We can look a bit deeper into the results and work out how likely different scorelines are:

Murray 2 – 0 Nadal: 30.3%
Murray 2 – 1 Nadal: 27.2%
Murray 1 – 2 Nadal: 22.3%
Murray 0 – 2 Nadal: 20.1%

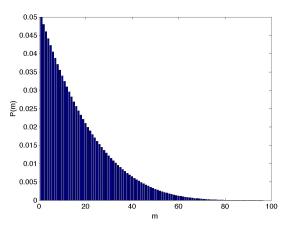
Another interesting stat is how many points we’d expect to see. In the following plot, we can see the number of points in each of the 10,000 simulated matches (the quality is a bit low – click the image to see a better version):

The red line shows the number in the actual match: 223. Only 1.6% of the simulated matches involved 223 or more points. So, if we’re happy that our model is realistic, the match was surprisingly long.

How realistic is the model? Not very. It’s based on the assumption that all points are independent of one another. In other words, the outcome of a particular point doesn’t depend on what’s already happened – an unrealistic assumption – players are affected by previous points. It also assumes that the chance of say, Murray winning a point when he is serving is constant throughout the match. This is also unrealistic – players get tired. These caveats don’t necessarily mean that the model is useless, but they should feature prominently in any conclusions.

One way to make it more realistic, would be to use the stats from the three different sets when performing the simulation. The stats for the three sets (from Murray’s point of view) are:
Set 1: Serving 28/36 (77.8%), Receiving 7/36 (19.4%)
Set 2: Serving 18/25 (72.0%), Receiving 14/30 (46.7%)
Set 3: Serving 32/53 (60.4%), Receiving 15/43 (34.9%)

Simulating 10,000 results with this enhanced model results in Murray winning 5932 matches (59.3%). This is slightly higher than the previous result but we’d need to simulate more matches to be sure it’s not just a bit higher by chance.

Here is the breakdown of the possible match scores:

Murray 2 – 0 Nadal: 40.2%
Murray 2 – 1 Nadal: 19.1%
Murray 1 – 2 Nadal: 37.5%
Murray 0 – 2 Nadal: 3.2%

This is very different to the previous breakdown. Scores of 2-0 and 1-2 have both become more likely and a Nadal 2-0 win looks very unlikely. We can see why if we look more closely at who wins each set. The first set is pretty close: Murray wins it 42.6% of the time. The second set is incredibly one-sided with Murray winning it 94.5% of the time. If the match goes to a third set, Murray wins it 34.1% of the time.

Interestingly, if we look at the number of points again, it’s now even less likely to see 223 or more points. Only 54 matches got this long (or longer) (0.5%). I didn’t expect this – my gut feeling as to why the matches in the first model were on the whole shorter than the real one was that the model wasn’t much good. However, this new model is more realistic, and the lengths have got shorter!

One possible conclusion to the whole analysis is that the scoreline was a bit flattering to Murray – he nearly one the third set although he didn’t play particularly well in it (he could expect to win it only 34.1% of the time). To illustrate how much better Nadal played in the final set we can simulate matches using just the stats from the last set. This results in a very one-sided picture with Nadal winning 7132 (71.3%)!

Obviously the earlier criticisms of the model still apply – we’re now assuming that within a set, each player has a constant probability of winning points. It’s easy to argue that this is still insufficient. However, it certainly provides some food for thought.